
The Number py
By Carlos Caballé Puig.
One sunny day, I was out walking with my wife, Maria Dolores, we wanted to see a new avenue where some stone benches had just been erected. So, we sat down for a while to enjoy the surroundings, when I noticed that the designer had made some geometric shapes in different coloured paving tiles from the rest, forming some squares with four tiles and others with twenty-five.
Looking more closely, I suddenly thought of the idea that the four paving tiles had a perimeter of 8 units and an area of 4 units of surface tiling, while the shapes with twenty-five tiles had a perimeter of 20 units and an area of 25 tiles.

Knowing maths, it was easy to find out the perimeter and surface area of the design, but what awoke my curiosity was the fact that the small shape had a larger perimeter than its surface area, and the large shape had a smaller perimeter than surface area. In view of the fact that all the paving tiles were the same, then it must be that a geometric shape exists with units of perimeter and units of area being equal.
When I got home, I sat down in front of a notebook, and with a pencil in my hand I started to calculate the mathematical values of some simple geometric shapes where the area was the same as the perimeter. However, there was nothing to relate the results to.
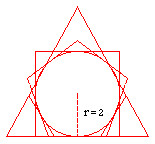
A few days later, I had the crazy idea of drawing the geometric shapes, and superimposing them. Imagine my surprise when I discovered that they all had an identical apothem value, with a result of 2 units. It was logical, given that all geometric shapes can be factorised in triangles, as there are the same amount of triangles of factorisation as the number of sides of the shape, and given that the area of a triangle is equal to half the value of its base times the product of its height, when the height of the sub-triangles is equal to two the perimeter is equal to the area.<
When checking that the apothem of each of the regular convex polygons coincided with the radius of the bi-equivalent circumference, a dilemma arose in my mind, in reality it was stimulating, observing a permutation between the definitions of apothem and radius. These concepts are changed in the bibliography. So that we can understand each other more clearly, the wheels on carriages have apothems in place of radiuses.
The word "apothem" comes from the Greek word "APÓ" which means far and "TÍZEMI" which means position. Being obvious that the farthest point from the centre of a polygon is the vertex of any one of its angles and never the centre of one of its sides, now, I don't need to quibble over the bibliographical definitions which took us so long to learn, because what I really want to do is work with the connection between both concepts or with the angle which they form, and although by definition the concepts between apothem and radius in any geometric shape are changed "π" will always be the result of a mutual connection.

Taking, as an example, the case of a square which I will factorise in four triangles as shown in the diagram, although any regular geometric shape would do, I will observe one of the interior triangles, checking that the apothem and radius form an angle, and all the angles between the apothems and radiuses add up to a value of 360°. The opening of each angle has as a tangent the quotient between mid side and the radius of the shape, with the number of internal triangles of factorisation being equal to the number of sides of the shape.
In any geometric shape, the apothem and radius form an angle equal to the quotient dividing 180° by the number of sides of the shape and its tangent is a universal constant which we can easily calculate.
If we multiply the number of sides of any regular geometric shape by the tangent which forms the apothem and its radius, we will obtain a different constant for each shape, and this value I will call "py" of the shape, that is why "π" is a connection between the apothem and radius, which has a numerical value the product of the number of sides of the shape times the tangent of the angle which is formed by the apothem and radius.
I can now conclude that although in the bibliography, the concepts between apothem and radius are changed, "π" is not a universal constant, but a mathematical connection which corresponds to an infinite series of constant polygons, and which has till now been "badly defined" one example of this is the circumference.
© Copyright C.C.P. - 2005